GW calculations via VASP

Contents

• Prerequisites
• Overview
• \(G_0W_0\) procedure
  • 1-DFT relaxation
  • 2-Exact diagonalization
  • 3-GW calculation
  • 4-Wannier90 band structure
• \(GW_0\) procedure

Prerequisites

This tutorial assumes the following are installed:

1. VASP 5.4 (preferred) or other versions 5.x (requires license)
2. Wannier90 v2.1 (link here)

Note that VASP GW calculations do not rely on Wannier90, but in order to do band structure calculations, Wannier90 must be installed and VASP must be re-compiled with reference to a Wannier90 library. See my instructions for installing VASP with Wannier90.

Overview

There are several different levels/types of GW calculations in VASP. A nice video describing the different levels of approximation in VASP is a lecture by Martijn Marsman:

The lecture slides in the video are available in pdf format.

Summary of tutorial

This tutorial covers \(G_0W_0\) (also known as single-shot GW) and \(GW_0\) calculations, with application to bulk 2H-MoS\(_2\). In the \(G_0W_0\) approximation, the random phase approximation (RPA) is used and the KS eigenvectors and eigenvalues are used directly to form the Green’s function \(G_0\) and screened Coulomb potential \(W_0\) (the subscript \(0\) indicates that no self-consistent cycle is performed). This may seem like a poor approximation, but it is the fastest computationally and gives results that improve over PBE for a number of semiconducting/insulating systems. Improvements are made in \(GW_0\), which involves self-consistently updating the eigenvalues in the computation of \(G\) while using the original KS eigenvectors and still in the RPA, hence the name \(GW_0\). Both methods and their relative agreements with experiment are discussed in a Phys. Rev. B article.

Ideally \(GW\) eigenvalues and eigenvectors would be updated self-consistently at each iteration and would be used to recompute both \(G\) and \(W\) separately. This has been explored in a Phys. Rev. Lett. article and shows that within the RPA, this will actually tend to worsen the results, i.e., overshoot the experimental bandgaps of most materials. This issue is alleviated when moving beyond the RPA by including other excitonic effects in the GW self-energy. In this case, the results are more closely aligned with experiment, but are very similar to those obtained by the \(GW_0\) method. The reason for this is likely error cancellation that results from using the RPA with the Kohn-Sham eigenvectors.

Below we specifically explore the \(G_0W_0\) case, but it is straight-forward to extend to the \(GW_0\) case (basically changing the tag NELM = 1 to NELM = 4 in the INCAR file, which allows for 4 electronic iterations to achieve self-consistency).

\(G_0W_0\) procedure

Tutorial files for this section are located here.

There are 4 steps that need to be done to perform a \(G_0W_0\) calculation, with an optional 5th step if the GW band structures are desired. Each of these are described below for bulk 2H-phase \(\mathrm{MoS}_2.\) The folders are set up as follows:

$ ls
1-relax/  2-scf/  3-diag/  4-gw/

Note that the KPOINTS and POTCAR files are stored only in 1-relax, while the other directories provide hard links to those files. Additionally, folders 2, 3, and 4 use a POSCAR that is a link to 1-relax/CONTCAR. Step 5 below (the Wannier90 band structure calculation) is done in the 4-gw folder.

1. DFT relaxation

Files for this section can be found here

Note that all calculations should use GW POTCAR files. In this case, we use Mo_sv_GW and S_GW. These are important because they reproduce scattering properties of the core to higher energies than the standard pseudopotentials (see the video/slides above for details).

The input file in 1-relax is:

SYSTEM  = MoTe2

NCORE  = 4
KPAR   = 9

ENCUT   = 400
IBRION  = 2
ISIF    = 3
ISYM    = 2
NSW     = 50

ISMEAR  = 0
SIGMA   = 0.05
#NBANDS  = 65
#NEDOS   = 3000

PREC    = Accurate
EDIFF   = 1.e-5
LREAL   = False
LASPH   = True

Note that the relaxation needs to be done multiple times, replacing the POSCAR file with the CONTCAR file. We do this until only 3 iterations are needed to converge. Without doing this, basis set errors will be present and the structure will not be fully relaxed.

We use a \(12\times12\times1\) k-point grid, since we should not need to account for dispersion along the out-of-plane direction. It turns out that this grid is sufficient for all calculations done, but in principle this should be tested for each material to ensure that the desired property (e.g., final GW band structure) does not change when the k mesh size increases. Here is the KPOINTS file:

MoS2
 0
Gamma
 12 12 1

For testing purposes, it can be faster to decrease to \(8\times8\times1\) or lower sizes.

2. SCF procedure

Files for this section can be found here.

To perform the GW calculation (step 4), we first perform a standard SCF cycle (IBRION=-1 in 2-scf) and then an exact diagonalization (ALGO=Exact in 3-diag) and save the WAVECAR file to disk. Note that the NBANDS flag must be set to something large for an accurate GW calculation (here we use 65; the total number of occupied states is 26, so this is over double that value, but this should be tested for convergence).

The 2-scf folder is useful for providing a starting set of wavefunctions for the exact diagonalization in 3-diag and also for computing the PBE band structures with Wannier90. The INCAR file in 2-scf is:

SYSTEM  = MoTe2

KPAR   = 20

ENCUT   = 400
IBRION  = -1
ISYM    = 2
NSW     = 1

ISMEAR  = 0
SIGMA   = 0.05
NBANDS  = 65
NEDOS   = 3000

PREC    = Accurate
EDIFF   = 1.e-8
LREAL   = False
LASPH   = True

LWAVE      = True
LWANNIER90 = True

Note that to do the Wannier90 procedure with VASP, a file named header.win or wannier90.win is needed prior to the start of the VASP calculation (see below in the GW section for more details):

Begin Projections
  Random
End Projections

guiding_centres = .true.

3. Exact diagonalization

Files for this section can be found here.

For the exact diagonalization in 3-diag, we point out that there are 2 different options in this step for preparing the GW calculation in step 3:

(a) Insulators and semiconductors: use LOPTICS=.TRUE., which will compute the frequency-dependent dielectric matrix and spit out a WAVEDER file that contains the derivatives of the KS orbitals with respect to \(\mathbf{k}\). These are then read in step 3 to construct the dielectric matrix.

(b) Metals: use LOPTICS = .FALSE.. VASP recommends using this for metals.

In either case, option (b) can be used, but GW calculations of semiconductors and insulators may converge faster using (a). Since MoS\(_2\) is a semiconductor, we use the following INCAR for this calculation:

SYSTEM = MoS2

NCORE  = 18
KPAR   = 8

# Freq.-dep. diel. tensor w/out local field effects
ALGO    = Exact
NBANDS  = 65
LOPTICS = True
CSHIFT  = 0.1

NELM  = 4

# you might try
#LPEAD = .TRUE.

ENCUT  = 400
EDIFF  = 1e-7
PREC   = Accurate
LREAL  = False
LASPH  = True

ISMEAR = 0
SIGMA  = 0.05
NEDOS  = 3000

LWAVE   = True

4. GW calculation

Files for this section can be found here

GW calculations can run in parallel, but only across k-points using KPAR. Therefore NCORE or NPAR > 1 will not work for GW. Note that KPAR specifies indirectly the number of cores that will work on a given k-point group. Since we are unable to parallelize by distributing plane-wave coefficients, it does not make sense to have more than one core work on a single k-point. Therefore, we should ideally use KPAR = # cores in this case. So if we are running VASP with mpirun -np 20, we should choose KPAR = 20. Obviously it does not make sense to request more cores than the total number of k points. Ideally, if we have N k-points, we would run VASP on N cores, and we would therefore choose KPAR = N, since this would effectively put every k-point calculation on a separate core.

Memory usage in \(G_0W_0\) is extremely important. GW calculations require allocation of a response function matrix, which scales like the number of GW G-vectors squared, specified by ENCUTGW. This matrix can typically be on the order of several GB, so that the amount of available memory can quickly be surpassed. VASP unfortunately does not provide any common-sense error handling when it tries to allocate more memory than is available, and only results in errors that typically say something like Virtual memory error. This indicates that you have asked for too much memory on a given node. The solution to this problem typically involves using FEWER cores per node than you have available. For example, assume that you have 32 k points and 36 cores per node, so you want to run VASP with KPAR = 32 and mpirun -np 32 vasp. This makes perfect sense, but unless you have a large amount of memory (RAM) on the node (on the order of 300 GB or more, assuming the total memory per MPI process is around 10 GB, which is typical), you will almost surely run into a memory error. The solution is to instead specify fewer cores per node and run on more nodes. In Slurm, one solution would be to set #SBATCH --nodes=3 and #SBATCH --ntasks-per-node=11, while still using mpirun -np 32 vasp. By doing this, you ensure that at most 11 MPI processes can run on a given node. If we assume around 10 GB of array allocations per MPI process, this corresponds to roughly 100 GB or so memory per node, which is much more reasonable, though potentially still too high for many platforms. In that case, try moving to more nodes with fewer cores per node.

VERY IMPORTANT: If you want a band structure plot, make sure you set the flag LWANNIER90=.TRUE. in the INCAR and create a file titled header.win or wannier90.win in the 3-gw directory that looks as follows:

Begin Projections
  Random
End Projections

guiding_centres = .true.

This file must be present prior to starting the GW calculation in VASP. VASP will then append to this file the relevant text to run Wannier90. Without this file, the resulting band structures will use the phase of the Bloch orbitals by default and the resulting band structure is meaningless. The tag guiding_centres = .true. is also extremely important, as it helps to prevent getting stuck in local minima in the Wannierization routines (it really should be set to true by default, but unfortunately is not).

The INCAR for this case is:

SYSTEM = MoS2
KPAR   = 20

MAXMEM = 12000

ALGO      = GW0
LSPECTRAL = True
NELM      = 1
NOMEGA    = 100

NBANDS = 65
NEDOS  = 3000

# update the quasiparticle energies in Green's function (GW0)
#NELM = 4

ENCUT  = 400
ISMEAR = 0
SIGMA  = 0.05
EDIFF  = 1e-7
LASPH  = True

LWANNIER90 = True

Again, note the LWANNIER90 tag at the bottom. This is necessary for VASP to use header.win (which is copied to wannier90.win) and append the relevant output to that file.

When running, be sure to write a shell script that first copies the WAVECAR and WAVEDER files from 2-diag (see an example shell script in the repo).

$ cp ../3-diag/WAVEDER .
$ cp ../3-diag/WAVECAR .

5. Wannier90 band structure

Files for this section can be found here

If the header.win or wannier90.win file described in step 3 was included before running VASP for the GW calculation, you should see after the VASP GW calculation that VASP appended text to the end of wannier90.win.

From here, there are two steps:

1. Run wannier90.x in this directory with the file as-is, i.e.,

    $ cd 4-gw
    $ wannier90.x wannier90
   

   This will take a little while depending on the size of the system. When finished, you should see some extra wannier90 files in the directory.

2. Now that the Wannier functions have been computed, we want to get the bands in a second running of Wannier90. This is done by editing the same wannier90.win file, adding the following lines anywhere in the file:

   # Bandstructure plot 
   restart         =  plot
   bands_plot      =  true
   begin kpoint_path
     G 0.0000   0.0000   0.0000   M 0.5000   0.0000   0.0000
     M 0.5000   0.0000   0.0000   K 0.3333   0.3333   0.0000
     K 0.3333   0.3333   0.0000   G 0.0000   0.0000   0.0000
     G 0.0000   0.0000   0.0000   A 0.0000   0.0000   0.5000
   end kpoint_path
   bands_num_points 40
   bands_plot_format gnuplot xmgrace 
   

The final result is a band structure that is shown here:

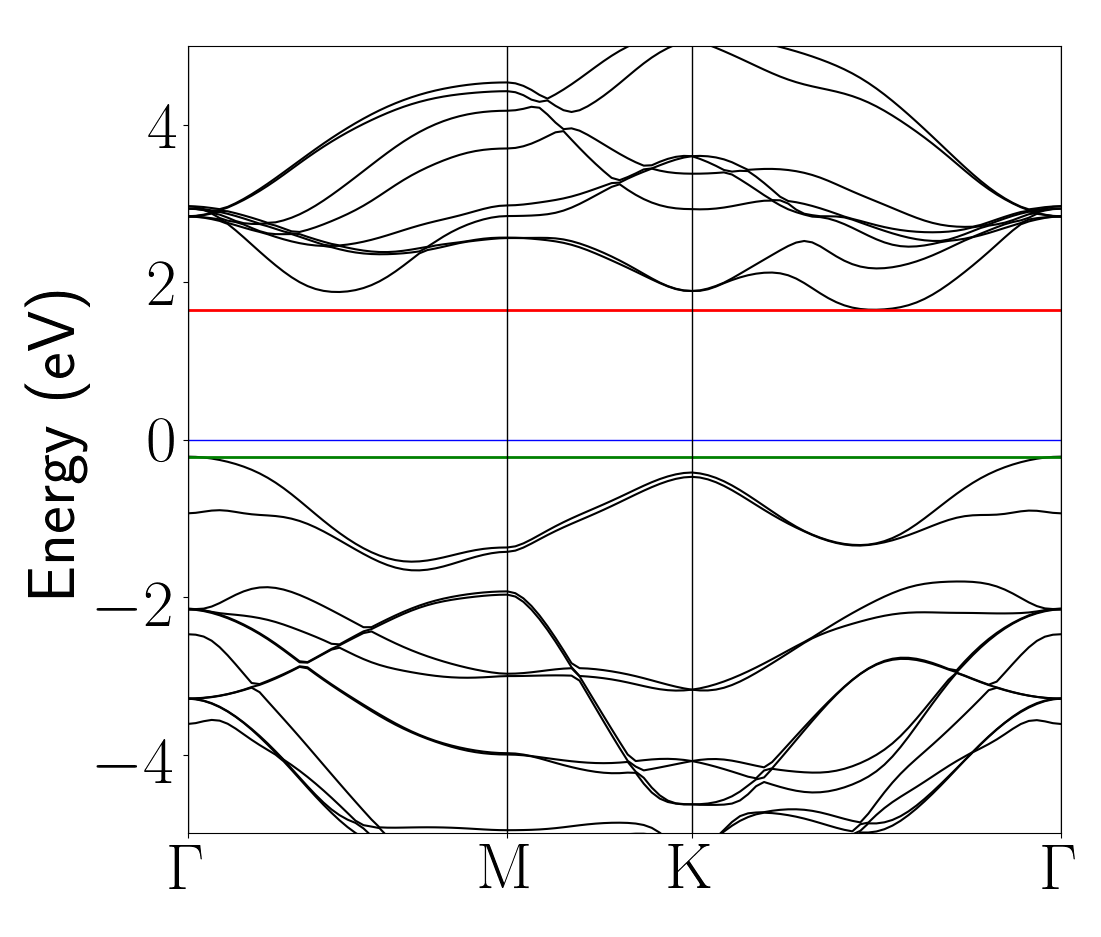
This result agrees fairly well with those presented in Phys. Rev. B 85, 205302 (2012).

\(GW_0\) procedure

To run \(GW_0\) instead of \(G_0W_0\), steps 1, 2, 3, and 5 are identical to the above. The only difference is that in step 4, the tag NELM = 1 should be changed to NELM = 4 or some other number greater than 1 (4 is recommended). Note that \(GW_0\) does not update the KS eigenvectors during the NELM self-consistent iterations, but only the KS eigenvalues. The reasons for the good agreement of \(GW_0\) with experiment likely has to do with fortuitous error cancellation that occurs when using the RPA with the KS eigenvectors and updating only the KS eigenvalues.